by Heitor Murilo Gomes, Albert Bifet on November 15, 2017 using MOA 2017.06.
1. Before you start
The focus of this tutorial is to show you how to easily simulate abrupt, gradual, incremental and mixed drifts on synthetic data streams using the MOA framework.
Disclaimer:
- This tutorial was originally developed for MOA Release 2016.04, but it also works with the current MOA 2017.06 version (obtain it in here). In fact, it shall work with previous and future releases as the drift simulation framework has been around for a while and is unlikely to change.
- We assume you are already familiar with what is a concept drift. In case you are not, then please refer to this paper [1]. Also, you will find useful material about how concept drifts are simulated in MOA in the “Data Stream Mining: A practical Approach” book, Chapter 2 (sections 2.7 and 2.7.1), which can be obtained for free in the Documentation page.
- All examples are presented using both the MOA GUI and the command line as well. To run the examples you must copy and paste the command line in the MOA GUI (see instructions in the “Running the examples” section).
- This tutorial does not cover the RecurrentConceptDriftStream class which allows easily simulating Recurrent Concept Drifts.
- We do not cover into details the evaluation method used. We simply use the default EvaluationPrequential configuration. Some comments are made about how it impacts the evaluation, but there is no thorough dis- cussion on this topic. We suggest this paper [2] for those interested in state-of-the-art evaluation procedures for data streams.
- To generate plots as those available in this tutorial use the script available here
Synthetic data stream generators are often used to evaluate machine learning algorithms for the data stream setting. One motivation for using synthetic data streams is that one can easily simulate different types of drifts on them, and use it to evaluate how a specific algorithm performs given different types of drifts. In this tutorial we are going to use 3 different generators: SEA [3], AGRAWAL [3] and HYPERPLANE [4].
This tutorial is divided into 6 sections. The first section briefly introduces how to run the examples in the MOA GUI and in the command line. In the second section we show how to simulate gradual and abrupt drifts. In the third section we show how to simulate gradual and abrupt drifts. The fourth section shows how to simulate incremental drifts. Section 5 shows how to save the synthetic data streams generated in the previous sections to ARFF (weka format) files which can then be used even outside MOA. Finally, the last section present exercises to practice your skills.
2. Running the examples
To run the examples you can either use the MOA GUI or the command line. To run them on the GUI the simplest approach is to copy and paste the command lines presented in each example. The whole process is as follows:
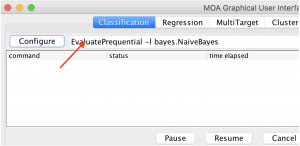
Right mouse click on the text input right next the Configure button as in Figure 1.
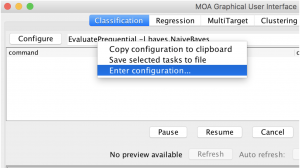
Choose “Enter configuration” as in Figure 2.
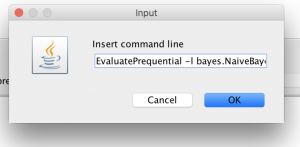
Paste the command line in the text dialog as in Figure 3.
To run the commands on the command line you will need to change direc- tory (cd or chdir depending on your operating system) to the location of the MOA jar and execute a command like the one shown below (replace the text within double quotes by the command given in the examples):
java -cp moa.jar moa.DoTask “EvaluatePrequential -l bayes.NaiveBayes -s (ConceptDriftStream -s (generators.SEAGenerator -f 3) -d (generators.SEAGenerator -f 2) -p 50000 -w 20000) -i 100000 -f 1000”
2.1 Optional: Configuring on the GUI
Optionally, you can configure a whole setting using the GUI. This is most likely what you will need to do if you want to configure a synthetic data stream to simulate drift yourself. A step-by-step is provided in the rest of this subsection.
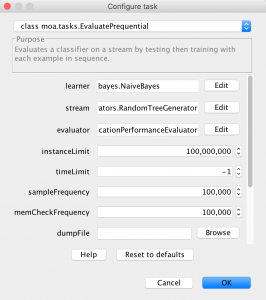
1) Choose the “Configure” button as shown in Figure 4.
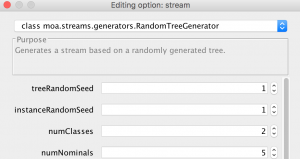
2) Select “Edit” on the Stream option. Make sure that you have EvaluatePre- quential or another evaluation method in the configuration drop down at the top. Notice that it is in the Task (in this case EvaluatePrequential) window that the total number of instances to be generated is selected using parameter instanceLimit.
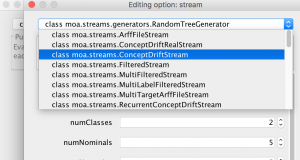
3) Change the data stream (the drop down at the top in Figure 6) to moa.streams.ConceptDriftStream as shown in Figure 7.
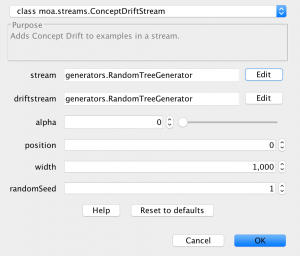
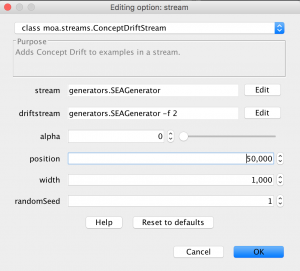
4) In Figure 8 the options for ConceptDriftStream are shown. Basically, it is important to configure the parameters:
- stream: The first concept will be generated using this stream configuration.
- driftstream: The next concept will be generated using this stream configuration.
- position: The location of center of the drift in terms of the number of instances.
- width: The length of the window of drift, i.e., the number of instances where the drift will take place.
Notice that the parameter alpha is also important to configure the underlying sigmoid function that models the transition between one concept to the other, however tweaking alpha is beyond the scope of this tutorial.
5) Finally, Figure 9 shows a possible configuration for a “one-drift” stream. In the rest of this tutorial other configurations are presented and commented, though it is important to mention that it is possible to configure another ConceptDriftStream in driftstream, thus allowing for multiple drifts to be simulated on the same stream.
3. Simulating Abrupt and Gradual Drifts
Basically, the experimental framework for inducing artificial concept drifts in MOA simulates a window of change where the probability of a given instance belonging to the current concept of the new concept is governed by a sigmoid function. Let’s name the current concept as A and the new concept as B, basically at the start of the window the probability that one instance is draw from A is higher, while at the end of the window the probability from it being draw from B increases, after the window is over all instances will be draw from B (the ”new concept” B is now stable).
3.1 Example 1: Gradual drift using SEA
In this example we use the SEA generator to create 100 thousand instances, such that there is a drift centered around instance 50,000 with a window of 20,000 instances.
The command line for Example 1 is shown below:
EvaluatePrequential -l bayes.NaiveBayes -s (ConceptDriftStream -s (gen- erators.SEAGenerator -f 3) -d (generators.SEAGenerator -f 2) -p 50000 -w 20000) -i 100000 -f 1000
The breakdown of these commands is as follows:
- EvaluatePrequential: The evaluation method used
- -l bayes.NaiveBayes: The learner used
- -i 100000 -f 1000: determines the total amount of instances to be gen- erated by the synthetic generator (-i parameter: 100 thousand) and the number of instances between reporting the evaluation metrics values (-f parameter: 1 thousand).
- -s (ConceptDriftStream -s (generators.SEAGenerator -f 3) -d (genera- tors.SEAGenerator -f 2) -p 50000 -w 20000): This is the most important part of the command for us in this tutorial as it configures how the drift is simulated. The parameter -s indicates that the following command is the configuration of the data stream to be used in the evaluation. We use the ConceptDriftStream, which is the main class for simulating drifts, notice how it has 2 data stream parameters -s and -d, such that the first corre- sponds to the current concept and the second one to the ’new concept’ or ’drift concept’. The parameters -p indicates the location of the drift within the data stream (i.e. the 50,000th instance) and -w indicates the number of instances in the drift window (i.e. 20k instances).
Finally,one important question is:“What is the difference between SEAGenerator -f 3 and SEAGenerator -f 2?” To simulate a concept drift we need to change the concept, to do that, we need a generator which has a con- figurable data distribution. In this case, SEA has four functions that can be variate to drastically change the underlying concept. In our example we change from SEA with function 3 to SEA with function 2.
Figure 10 shows the results of Example 1. Notice how the accuracy starts to drop within the window of drift and how it does not recover from it as the classifier used (Naive Bayes) does not implement any drift adaptation technique.
Sometimes this might not happen because the classifier selected does include a built-in drift adaptation technique.
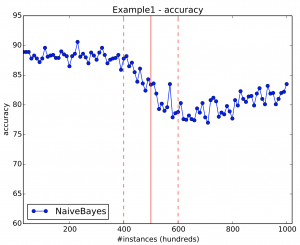
Figure 10: Example 1 results. Solid and dashed vertical red lines indicates drifts and drift window start/end, respectively.
3.2 Example 2: Abrupt drift using SEA
To simulate abrupt drifts, one just need to set the drift length to 1, in other words, set -w to 1. We use the same command as in Example 1 with the only difference being the drift window size.
The command line for Example 2 is shown below:
EvaluatePrequential -l bayes.NaiveBayes -s (ConceptDriftStream -s (gen- erators.SEAGenerator -f 3) -d (generators.SEAGenerator -f 2) -p 50000 -w 1) -i 100000 -f 1000
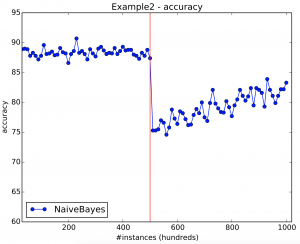
Figure 11 shows the results of Example 2. Notice that after the drift there is a steep decrease in accuracy.
4. Simulating Multiple and Mixed Drifts
The MOA drift simulation framework can easily be extended to simulate various drifts on the same data stream with drifts on different locations of the stream. In the following examples we show how it can be used to simulate streams with multiple abrupt drifts (which could also be gradual) and mixed abrupt and gradual drifts.
4.1 Example 3: Multiple Abrupt Drifts
In this example we are going to use the AGRAWAL generator. The ‘catch’ to simulate multiple drifts is to use the ConceptDriftStream class recursively. In this example we also present the results for a classic ensemble classifier method that can cope with concept drifts, i.e., the Leveraging Bagging [5] algorithm.
The command for Example 3 using Naive Bayes is shown below:
EvaluatePrequential -l bayes.NaiveBayes -s (ConceptDriftStream -s gen- erators.AgrawalGenerator -d (ConceptDriftStream -s (generators.AgrawalGenerator -f 2) -d (ConceptDriftStream -s generators.AgrawalGenerator -d (generators.AgrawalGenerator -f 4) -p 25000 -w 1) -p 25000 -w 1) -p 25000 -w 1) -i 100000 -f 1000
The command for Example 3 using Leveraging Bagging is shown below:
EvaluatePrequential -l meta.LeveragingBag -s (ConceptDriftStream -s generators.AgrawalGenerator -d (ConceptDriftStream -s (generators.AgrawalGenerator -f 2) -d (ConceptDriftStream -s generators.AgrawalGenerator -d (generators.AgrawalGenerator -f 4) -p 25000 -w 1) -p 25000 -w 1) -p 25000 -w 1) -i 100000 -f 1000
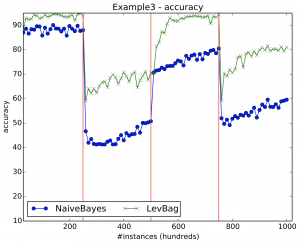
Figure 12 shows the results for Naive Bayes and Leveraging Bagging for the AGRAWAL data stream with 3 abrupt concept drifts. Notice how Leveraging Bagging recover from drifts better than Naive Bayes.
4.2 Example 4: Mixed Drifts
This example is really similar to Example 3 with the only exception that the first and last drifts are gradual instead of abrupt.
The command for Example 4 using Naive Bayes is shown below:
EvaluatePrequential -l bayes.NaiveBayes -s (ConceptDriftStream -s generators.AgrawalGenerator -d (ConceptDriftStream -s (generators.AgrawalGenerator -f 2) -d (ConceptDriftStream -s generators.AgrawalGenerator -d (generators.AgrawalGenerator -f 4) -p 25000 -w 10000) -p 25000 -w 1) -p 25000 -w 10000) -i 100000 -f 1000
The command for Example 4 using Leveraging Bagging is shown below:
EvaluatePrequential -l meta.LeveragingBag -s (ConceptDriftStream -s generators.AgrawalGenerator -d (ConceptDriftStream -s (generators.AgrawalGenerator -f 2) -d (ConceptDriftStream -s generators.AgrawalGenerator -d (generators.AgrawalGenerator -f 4) -p 25000 -w 10000) -p 25000 -w 1) -p 25000 -w 10000) -i 100000 -f 1000
Figure 13 presents the results for Leveraging Bagging and Naive Bayes us- ing an AGRAWAL data stream with 2 gradual drifts and 1 abrupt drift.

Figure 13: Example 4 results. Solid and dashed vertical red lines indicates drifts and drift window start/end, respectively. The drift in the middle as an abrupt drift, the dashed lines to its right and left are respectively the end and start of the other gradual drifts in this experiment.
5. Simulating Incremental Drifts
It would not be practical to use the same generic framework to simulate incremental drifts as we have been using for abrupt and gradual drifts. Therefore, incremental drifts are simulated within the data stream generator algorithm. In this section we will use HYPERPLANE generator to simulate incremental drifts by varying the values of the hyperplane weights as the data stream advances. A hyperplane is a flat, n − 1 dimensional subset of that space that divides it into two disconnected parts. It is possible to change a hyperplane orientation and position by slightly changing its relative size of the weights wi.
5.1 Example 5: Incremental Drifts
The command for Example 5 is shown below:
EvaluatePrequential -l bayes.NaiveBayes -s (generators.HyperplaneGenerator -k 10 -t 0.01 -s 10) -i 100000 -f 1000
Two important parameters in this command are -t and -s, which control the magnitude of change after every instance and the probability that the change direction is reversed, respectively.
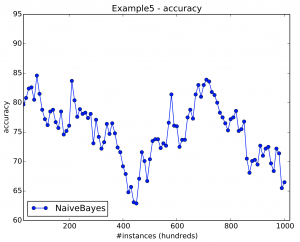
Figure 14 shows the results for Example 5.
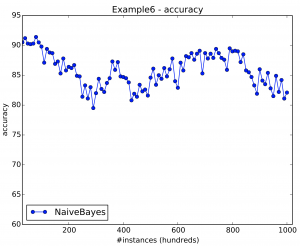
5.2 Example 6: Subtle Incremental Drifts
If we desire to simulate subtle incremental drifts using HYPERPLANE gener- ator we can decrease the magnitude of change, i.e., parameter -t.
EvaluatePrequential -l bayes.NaiveBayes -s (generators.HyperplaneGenerator -k 10 -t 0.001 -s 10) -i 100000 -f 1000
6. Saving the Synthetic Streams to ARFF files
Finally, you might want to export the data streams you generated to a file to, for example, open it on WEKA or in other software that is compatible with the ARFF format. It is a rather easy task in MOA, the only thing that you need to change is the MoaTask from EvaluatePrequential to WriteStreamToARFF- File, remove the classifier specification (-l parameter), add the destination (-f parameter) file and the maximum number of instances (-m parameter).
Notice that the -f parameter in WriteToStreamARFFile is completely different from the Eval- uatePrequential -f parameter which indicates the sample frequency for evaluations. In fact, there is no reason to have a sample frequency in WriteToStreamARFFFile as we are generating the files and not evaluating the data stream.)
Sometimes people are confused about -m parameter as in the EvaluatePrequential the parameter to control the number of instances is -i.
Below you can find all the WriteToStreamARFFFile commands to export all the data streams previously generated in this tutorial.
Example 1:
WriteStreamToARFFFile -s (ConceptDriftStream -s (generators.SEAGenerator -f 3) -d (generators.SEAGenerator -f 2) -p 50000 -w 20000) -f example1.arff -m 100000
Example 2:
WriteStreamToARFFFile -s (ConceptDriftStream -s (generators.SEAGenerator -f 3) -d (generators.SEAGenerator -f 2) -p 50000 -w 1) -f example2.arff -m 100000
Example 3:
WriteStreamToARFFFile -s (ConceptDriftStream -s generators.AgrawalGenerator -d (ConceptDriftStream -s (generators.AgrawalGenerator -f 2) -d (ConceptDriftStream -s generators.AgrawalGenerator -d (generators.AgrawalGenerator -f 4)
-p 25000 -w 1) -p 25000 -w 1) -p 25000 -w 1) -f example3.arff -m 100000
Example 4:
WriteStreamToARFFFile -s (ConceptDriftStream -s generators.AgrawalGenerator -d (ConceptDriftStream -s (generators.AgrawalGenerator -f 2) -d (ConceptDriftStream -s generators.AgrawalGenerator -d (generators.AgrawalGenerator -f 4)
-p 25000 -w 10000) -p 25000 -w 1) -p 25000 -w 10000) -f example4.arff -m 100000
Example 5
WriteStreamToARFFFile -s (generators.HyperplaneGenerator – k 10 -t 0.01 -s 10) -f example5.arff -m 100000
Example 6
WriteStreamToARFFFile -s (generators.HyperplaneGenerator – k 10 -t 0.001 -s 10) -f example6.arff -m 100000
7 Exercises
7.1 Simulate 1 abrupt drift
Use generators.SEAGenerator to simulate 1 abrupt drift.
- The data should amount to 100 thousand instances;
- The drift should occur at instance 50,000;
- Generate the first concept using SEA function 1,while the second concept should be generated using SEA function 2;
- Evaluate the stream using EvaluatePrequential every 1,000 instances and a HoeffdingTree.
If you do not change parameters, except for those required in the exercise, then your final results would look like Figure 16.
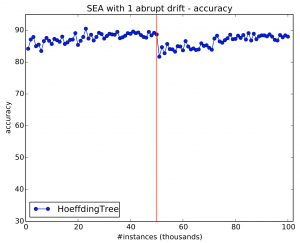
Figure 16: Simulating 1 drift using SEA generator. The solid vertical red line indicates drift location.
7.2 Simulate 2 gradual drifts with different widths
Use generators.SEAGenerator to simulate 2 gradual drifts, such that the drift window is different from one another.
- The data should amount to 1 million instances;
- Drifts should occur at 250k (window of size 50k) and 600k (window of size 200k);
- Generate the first concept using SEA function 1,the second concept using SEA function 2, and the final concept using function 3;
- Evaluate the stream using EvaluatePrequential every 10,000 instances and a HoeffdingTree.
If you do not change parameters, except for those required in the exercise, then your final results would look like Figure 17.
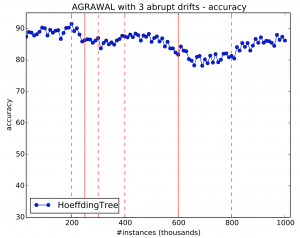
Figure 17: Simulating 2 drifts using SEA generator. Solid and dashed vertical red lines indicates drifts and drift window start/end, respectively.
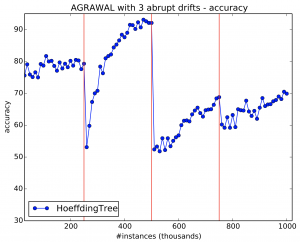
7.3 Simulate 3 abrupt drifts
Use generators.AgrawalGenerator to simulate 3 abrupt drifts.
- The data should amount to 1 million instances;
- Drifts should occur every 250,000 instances (i.e. at 250k, 500k and 750k);
- The concepts should be different from one another. Precisely change the function (parameter -f) in Agrawal, such that the first concept uses function 5, the second function 3, the third function 2 and the fourth function 6;
- Evaluate the stream using EvaluatePrequential every 10,000 instances and a HoeffdingTree.
If you do not change parameters, except for those required in the exercise, then your final results would look like Figure 18. Notice the sudden drops in accuracy after every drift.
References
[1] João Gama, Indre Zliobaite, Albert Bifet, Mykole Pechenizkiy, and Abderl- hamid Bouchachia. A survey on concept drift adaptation. ACM Computing Surveys, 46(4):44:1–44:37, 2014.
[2] Albert Bifet, Gianmarco de Francisci Morales, Jesse Read, Geoff Holmes, and Bernhard Pfahringer. Efficient online evaluation of big data stream classifiers. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 59–68. ACM, 2015.
[3] Rakesh Agrawal, Tomasz Imilielinski, and Arun Swani. Database mining: A performance perspective. IEEE Trans. on Knowledge and Data Engineering, 5(6):914–925, 1993.
[4] Geoff Hulten,Laurie Spencer, and Pedro Domingos.Mining time-changing data streams. In Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining, pages 97–106. ACM, 2001.
[5] Albert Bifet, Geoff Holmes, and Bernhard Pfahringer. Leveraging bagging for evolving data streams. In PKDD, pages 135–150, 2010.