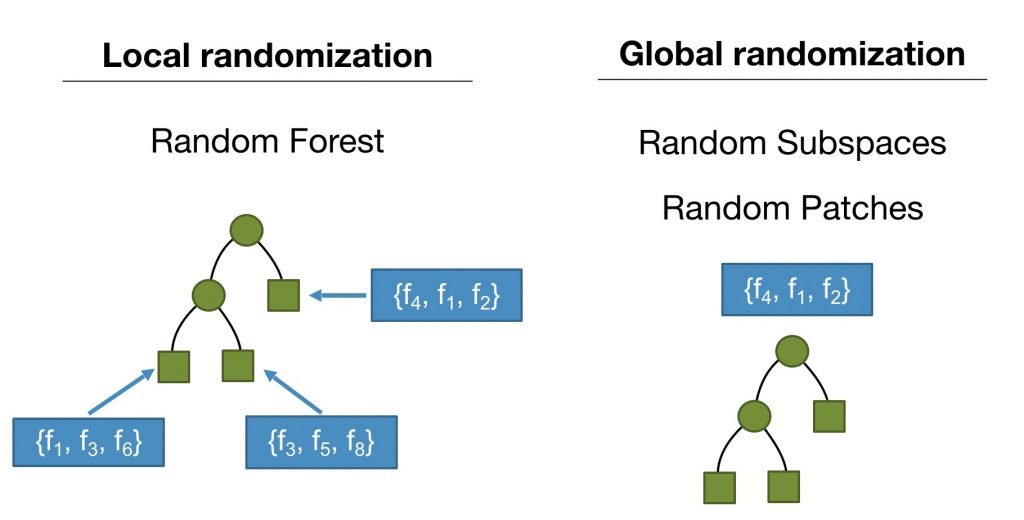
In the latest version of MOA, we added the Streaming Random Patches (SRP) algorithm [1]. SRP is an ensemble classifier specially designed to deal with evolving data streams that outperforms several state-of-the-art ensembles. It also shares some similarities with the Adaptive Random Forest (ARF) algorithm [2] as both use the same strategy for detecting and reacting to concept drifts. One crucial difference is that ARF relies on local subspace randomization, i.e. random subsets of features are set for each leaf to be considered for future node splits. SRP uses a global subspace randomization, as in the Random Subspaces Method [3] and Random Patches [4], such that each base model is trained on a randomly selected subset of features. This is illustrated in the figure below:
SRP predictive performance tends to increase as we add more learners, which is an essential characteristic of an ensemble method, and it is not achieved by many existing ensemble methods designed for data streams. This was observed in a comparison against state-of-the-art classifiers in a multitude of datasets presented in [1].
Another attractive characteristic is that SRP can use any base model, as it is not constrained to decision trees as ARF.
SRP Options in MOA
SRP is configurable using the following options in MOA:
- treeLearner (-l). The base learner. Default to a Hoeffding Tree, but it is not restricted to decision trees.
- ensembleSize (-s). The number of learners in the ensemble.
- subspaceMode (-o). Defines how m, defined by mFeaturesPerTreeSize, is interpreted. Four options are available: “Specified m (integer value)”, “sqrt(M)+1”, “M-(sqrt(M)+1)”, “Percentage (M * (m / 100))”, such that M represents the total number of features.
- subspaceSize (-m). The number of features per subset for each classifier. Negative values are interpreted as M – m, such that M and m represents the total number of features and the subspace size, respectively. Important: This hyperparameter is interpreted according to subspaceMode (-o).
- trainingMethod (-t). The training method to use: Random Patches (SRP), Random Subspaces (SRS) or Bagging (BAG).
- lambda (-a). The lambda parameter for online sampling with reposition simulation.
- driftDetectionMethod (-x). Change detector for drifts and its parameters. Best results tend to be obtained by using ADWINChangeDetector, the default deltaAdwin (ADWIN parameter) is 0.00001. Still other drift detection methods can be easily configured and used, such as PageHinkley, DDM, EDDM, etc.
- warningDetectionMethod (-p). Change detector for warnings and its parameters.
- disableWeightedVote (-w). Whether to weigh votes according to base models estimated accuracy or not. If set, majority vote is used.
- disableDriftDetection (-u). Should use drift detection? If disabled, then the warning detector and background learners are also disabled. The default is to use drift detection, thus this is not set.
- disableBackgroundLearner (-q). Should use background learner? If disabled, then base models are reset immediately. The default is to use background learners, thus this is not set.
Using StreamingRandomPatches (SRP) and its variants
In this post, we are only going to show some examples of how SRP can be used as an off-the-shelf classifier and how to change its options. For a complete benchmark against other state-of-the-art algorithms, please refer to [1]. A practical way to test SRP (or any stream classifier) in MOA is to use the EvaluatePrequential or EvaluateInterleavedTestThenTrain tasks and assess its performance in terms of Accuracy, Kappa M, Kappa T, and others.
In [1], three variations of the ensemble were evaluated: SRP, SRS and BAG.
- SRP trains each learner with a different “patch” (a subset of instances and features);
- SRS trains on different subsets of features;
- BAG* trains only on a random subset of instances.
Important: SRP and BAG require more computational resources in comparison to SRS. This is due to the sampling with reposition method to simulate online bagging. Given the results presented in [1], SRS obtains a good trade-off in terms of predictive performance and computational resources usage.
To test StreamingRandomPatches you can copy and paste the following commands in the MOA GUI (right click the configuration text edit and select “Enter configuration”). All of the following executions use the electricity dataset (i.e. elecNormNew)(available here).
Test 1: SRP trained using 10 base models.
EvaluateInterleavedTestThenTrain -l (meta.StreamingRandomPatches -s 10) -s (ArffFileStream -f elecNormNew.arff) -f 450
Test 2: SRS trained using 10 base models.
EvaluateInterleavedTestThenTrain -l (meta.StreamingRandomPatches -s 10 -t (Random Subspaces)) -s (ArffFileStream -f elecNormNew.arff) -f 450
Test 3: BAG trained using 10 base models.
EvaluateInterleavedTestThenTrain -l (meta.StreamingRandomPatches -s 10 -t (Resampling (bagging))) -s (ArffFileStream -f elecNormNew.arff) -f 450
Explanation: All these commands executes InterleavedTestThenTrain on the elecNormNew dataset (-f elecNormNew.arff) using 10 base models and subsets of features with 60% of the total amount of features.
They only vary the training mode, i.e. SRP (default option, no need to specify -t), SRS “-t (Random Subspaces)” or BAG “-t (Resampling (bagging))”
Notice that the default subspaceMode (-o) is (Percentage (M * (m / 100)) and the subspaceSize (-m) is 60, which translates to “60% of the total features M will be randomly selected for training each base model.”
The subspaceMode and subspaceSize have a large influence in the performance of the ensemble. For example, if we set it to -o (Specified m (integer value)) -m 2, as shown below, we will notice a decrease in accuracy as 2 features per base model are not sufficient to build reasonable models for this dataset.
EvaluateInterleavedTestThenTrain -l (meta.StreamingRandomPatches -s 10 -o (Specified m (integer value)) -m 2) -s (ArffFileStream -f elecNormNew.arff) -f 450
The source code for StreamingRandomPatches is already available in MOA (StreamingRandomPatches.java).
[1] Heitor Murilo Gomes, Jesse Read, and Albert Bifet. “Streaming random patches for evolving data stream classification.” In 2019 IEEE International Conference on Data Mining (ICDM), pp. 240-249. IEEE, 2019.
[2] Heitor Murilo Gomes, Albert Bifet, Jesse Read, Jean Paul Barddal, Fabricio Enembreck, Bernhard Pfahringer, Geoff Holmes, Talel Abdessalem. “Adaptive random forests for evolving data stream classification”. In Machine Learning, DOI: 10.1007/s10994-017-5642-8, Springer, 2017.
[3] Tin Kam Ho. “The random subspace method for constructing decision forests.” IEEE transactions on pattern analysis and machine intelligence, 1998.
[4] Gilles Louppe and Pierre Geurts. “Ensembles on random patches.” In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pp. 346-361. Springer, 2012.
* BAG is not “bagging” per se as it includes the drift recovery dynamics and weighted vote from [1,2]. A precise naming would be something like “sampling with reposition” or “resampling” or any other name that only refers to how instances and features are organized for training each base model.
 The fame of the moa and the fact that its size made it a world-beater gave it the brief status of national symbol briefly in the 19th century. In the 1890s, New Zealand was ‘the land of the moa’, and of 103 entries for a new national coat of arms in 1906–8, 28 included moa. Moa also featured on commercial logos, and in cartoons to represent New Zealand. Its iconic status did not last, however, and was soon replaced by the kiwi.
The fame of the moa and the fact that its size made it a world-beater gave it the brief status of national symbol briefly in the 19th century. In the 1890s, New Zealand was ‘the land of the moa’, and of 103 entries for a new national coat of arms in 1906–8, 28 included moa. Moa also featured on commercial logos, and in cartoons to represent New Zealand. Its iconic status did not last, however, and was soon replaced by the kiwi.